Statistics 1

Jeff Stevens

2025-05-07

Set-up

Install and load packages

First, install these packages

install.packages(c("afex", "easystats"))

And load tidyverse

Create full data set

set.seed(1234) # this just means we'll always get the same random numbers
num_subjects <- 18
rtnorm <- function(n, mean = 0, sd = 1, min = 1, max = 5) {
  bounds <- pnorm(c(min, max), mean, sd)
  u <- runif(n, bounds[1], bounds[2])
  qnorm(u, mean, sd)}
my_data <- data.frame(subject = rep(1:num_subjects, each = 3),  # create subject column
                      gender = factor(rep(c("Female", "Male", "Nonbinary"), each = num_subjects)), # create gender column
                      age = factor(rep(c("Old", "Young"), each = num_subjects / 2)),  # create age column
                      time = rep(c(1:3), times = num_subjects / 2),  # create time column
                      response = rtnorm(num_subjects * 3, mean = 3.5, sd = 0.75),  # create response column
                      rt = round(rpois(num_subjects * 3, lambda = 100) * 10 + 1000, 1),  # create response time column
                      binary = sample(x = c(0, 1), size = num_subjects * 3, replace = TRUE))  # create binary response column
head(my_data)
  subject gender age time response   rt binary
1       1 Female Old    1 2.586046 1890      0
2       1 Female Old    2 3.706176 2060      1
3       1 Female Old    3 3.681445 2100      1
4       2 Female Old    1 3.708237 2330      1
5       2 Female Old    2 4.250138 1830      0
6       2 Female Old    3 3.740756 2120      1

Create data set for just time 1

my_data1 <- my_data |>
  filter(time == 1)
head(my_data1)
  subject gender   age time response   rt binary
1       1 Female   Old    1 2.586046 1890      0
2       2 Female   Old    1 3.708237 2330      1
3       3 Female   Old    1 1.746820 2070      1
4       4 Female Young    1 3.505189 2140      0
5       5 Female Young    1 3.055292 1950      1
6       6 Female Young    1 4.181727 1940      0

Create between-subjects data

my_data_between <- my_data1 |>
  select(age, response) |>
  arrange(age) |>
  mutate(id = rep(1:9, 2)) |>
  pivot_wider(names_from = age, values_from = response) |>
  select(-id)
head(my_data_between)
# A tibble: 6 × 2
    Old Young
  <dbl> <dbl>
1  2.59  3.51
2  3.71  3.06
3  1.75  4.18
4  2.82  4.44
5  3.10  3.40
6  2.91  3.49

Create within-subject/paired data

my_data_paired <- my_data |>
  filter(time != 3) |>
  pivot_wider(id_cols = subject, names_from = time, names_prefix = "time_", values_from = response)
head(my_data_paired)
# A tibble: 6 × 3
  subject time_1 time_2
    <int>  <dbl>  <dbl>
1       1   2.59   3.71
2       2   3.71   4.25
3       3   1.75   2.94
4       4   3.51   3.85
5       5   3.06   4.47
6       6   4.18   3.06

Descriptive statistics

Measures of central tendency

## Mean
mean(my_data$rt)
[1] 2012.037
## Median
median(my_data$rt)
[1] 2010
## Mode
mode_stat <- function(x) {
  ux <- unique(x)
  tab <- tabulate(match(x, ux))
  ux[tab == max(tab)]
}
mode_stat(my_data$rt)
[1] 2010

Measures of dispersion/error

# Standard deviation
sd(my_data$rt)
[1] 113.2434
## Standard error of the mean
sem <- function(x) {
  sd(x) / sqrt(length(x))
}
sem(my_data$rt)
[1] 15.41048

Summaries

## Interquartile range
IQR(my_data$rt)
[1] 145
## Quantiles
quantile(my_data$rt, probs = c(0.25, 0.5, 0.75))
   25%    50%    75% 
1922.5 2010.0 2067.5 
## Overall summary
summary(my_data$rt)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1820    1922    2010    2012    2068    2330

Confidence intervals

Between-subjects CIs

By hand

confidence_interval <- function(x, prob = 0.95) {
  qt((prob + 1) / 2, df = length(x) - 1) * sd(x) / sqrt(length(x))
}
confidence_interval(my_data$response)
[1] 0.1691312

From {papaja}

papaja::ci(my_data$response)
[1] 0.1691312

Incorporate into tidyverse

(gender_differences <- my_data |> # create tibble of means per gender
    group_by(gender) |> # for each level of gender column
    summarize(resp_means = mean(response), # calculate mean response
              resp_cis = papaja::ci(response) # calculate between-subjects confidence intervals
    ))
# A tibble: 3 × 3
  gender    resp_means resp_cis
  <fct>          <dbl>    <dbl>
1 Female          3.44    0.326
2 Male            3.23    0.315
3 Nonbinary       3.49    0.283

Within-subjects confidence intervals

Use wsci() from {papaja}

wsci(data = my_data, id = "subject", factors = "time", dv = "response")
  time  response
1    1 0.3102703
2    2 0.2723202
3    3 0.3684559
# Wrap it in summary() to include the means and generate the lower and upper limits
summary(wsci(data = my_data, id = "subject", factors = "time", dv = "response"))
  time     mean lower_limit upper_limit
1    1 3.254368    2.944098    3.564638
2    2 3.558330    3.286010    3.830650
3    3 3.343698    2.975242    3.712154

Correlations

Correlation matrix

cor(x = my_data[, c("response", "rt")])
           response         rt
response 1.00000000 0.07994129
rt       0.07994129 1.00000000

OR

my_data |>
  select(response, rt) |>
  cor()
           response         rt
response 1.00000000 0.07994129
rt       0.07994129 1.00000000

Correlation coefficient for single correlation

cor(x = my_data$response, y = my_data$rt)
[1] 0.07994129

Correlation hypothesis test

(cortest1 <- cor.test(my_data$response, my_data$rt))  # works with columns

    Pearson's product-moment correlation

data:  my_data$response and my_data$rt
t = 0.57832, df = 52, p-value = 0.5655
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1919275  0.3404152
sample estimates:
       cor 
0.07994129 
cor.test(~ response + rt, data = my_data)  # or formula

    Pearson's product-moment correlation

data:  response and rt
t = 0.57832, df = 52, p-value = 0.5655
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1919275  0.3404152
sample estimates:
       cor 
0.07994129

Non-parametric correlations

cor.test(my_data$response, my_data$rt, method = "kendall")

    Kendall's rank correlation tau

data:  my_data$response and my_data$rt
z = 0.89686, p-value = 0.3698
alternative hypothesis: true tau is not equal to 0
sample estimates:
       tau 
0.08514648 
cor.test(my_data$response, my_data$rt, method = "spearman")

    Spearman's rank correlation rho

data:  my_data$response and my_data$rt
S = 24000, p-value = 0.5402
alternative hypothesis: true rho is not equal to 0
sample estimates:
       rho 
0.08519906

Extracting statistics

str(cortest1)
List of 9
 $ statistic  : Named num 0.578
  ..- attr(*, "names")= chr "t"
 $ parameter  : Named int 52
  ..- attr(*, "names")= chr "df"
 $ p.value    : num 0.566
 $ estimate   : Named num 0.0799
  ..- attr(*, "names")= chr "cor"
 $ null.value : Named num 0
  ..- attr(*, "names")= chr "correlation"
 $ alternative: chr "two.sided"
 $ method     : chr "Pearson's product-moment correlation"
 $ data.name  : chr "my_data$response and my_data$rt"
 $ conf.int   : num [1:2] -0.192 0.34
  ..- attr(*, "conf.level")= num 0.95
 - attr(*, "class")= chr "htest"

Extracting statistics

papaja::apa_print(cortest1)
$estimate
[1] "$r = .08$, 95\\% CI $[-.19, .34]$"

$statistic
[1] "$t(52) = 0.58$, $p = .566$"

$full_result
[1] "$r = .08$, 95\\% CI $[-.19, .34]$, $t(52) = 0.58$, $p = .566$"

$table
A data.frame with 5 labelled columns:

  estimate    conf.int statistic df p.value
1      .08 [-.19, .34]      0.58 52    .566

estimate : $r$ 
conf.int : 95\\% CI 
statistic: $t$ 
df       : $\\mathit{df}$ 
p.value  : $p$ 
attr(,"class")
[1] "apa_results" "list"

Extracting statistics

papaja::apa_print(cortest1)$full
[1] "$r = .08$, 95\\% CI $[-.19, .34]$, $t(52) = 0.58$, $p = .566$"
cocoon::format_stats(cortest1)
[1] "_r_ = .08, 95% CI [-0.19, 0.34], _p_ = .566"

{correlation} package

From easystats 

# install.packages("correlation")
library(correlation)
(cortest2 <- cor_test(my_data, "response", "rt"))
Parameter1 | Parameter2 |    r |        95% CI | t(52) |     p
--------------------------------------------------------------
response   |         rt | 0.08 | [-0.19, 0.34] |  0.58 | 0.566

Observations: 54

Also runs correlation matrices, partial correlations, Bayesian correlations

Plot correlations

plot(cortest2)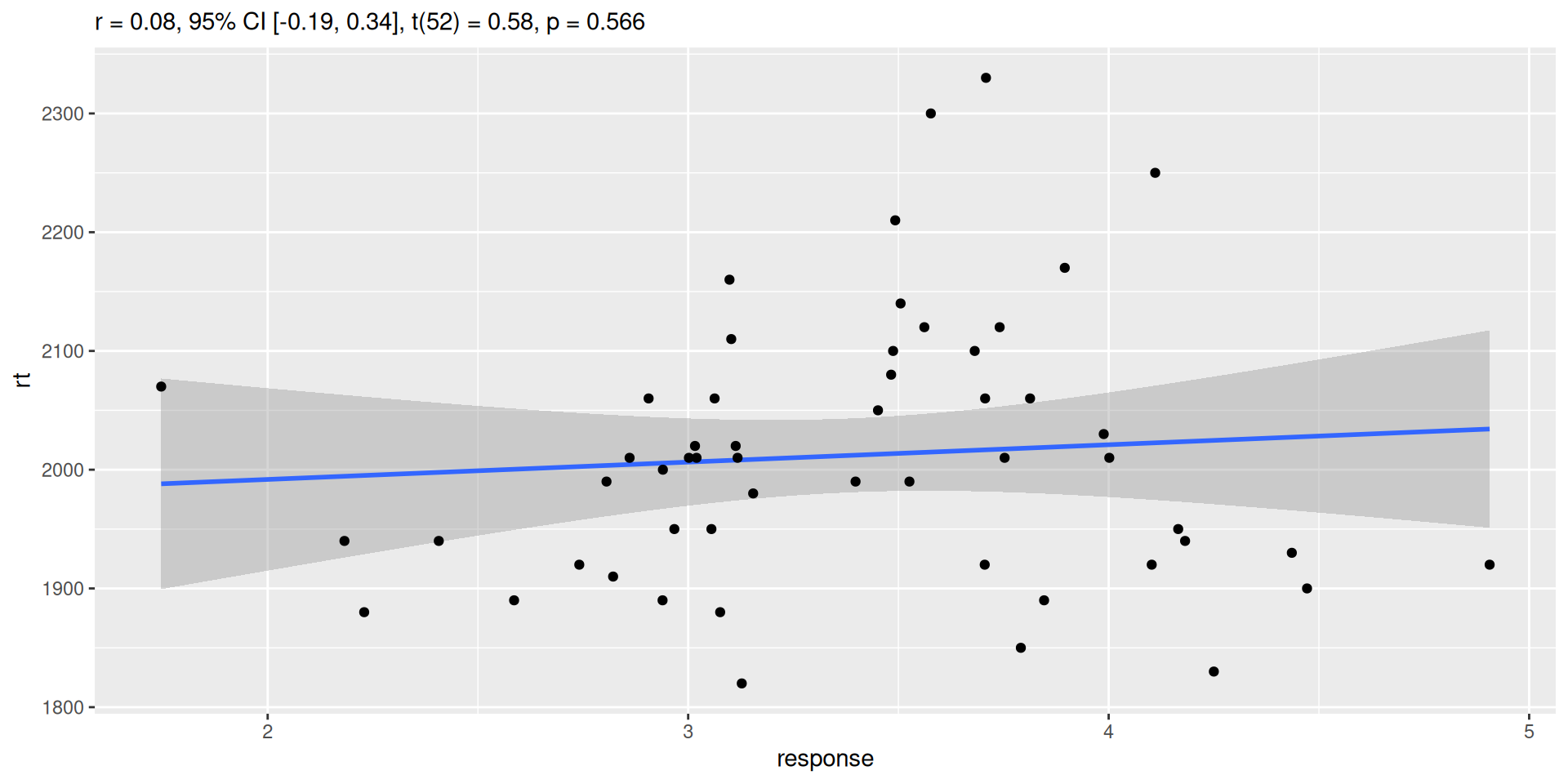

Parametric t-tests

One-sample t-test

t.test(my_data$response, mu = 3)

    One Sample t-test

data:  my_data$response
t = 4.5713, df = 53, p-value = 2.942e-05
alternative hypothesis: true mean is not equal to 3
95 percent confidence interval:
 3.216334 3.554596
sample estimates:
mean of x 
 3.385465

Two-sample, independent t-test

Variance not assumed to be equal (default)

t.test(my_data_between$Young, my_data_between$Old)  # works with columns

    Welch Two Sample t-test

data:  my_data_between$Young and my_data_between$Old
t = 1.8791, df = 14.815, p-value = 0.08005
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.0705276  1.1113499
sample estimates:
mean of x mean of y 
 3.514574  2.994162 
t.test(response ~ age, data = my_data1)  # and with formulas

    Welch Two Sample t-test

data:  response by age
t = -1.8791, df = 14.815, p-value = 0.08005
alternative hypothesis: true difference in means between group Old and group Young is not equal to 0
95 percent confidence interval:
 -1.1113499  0.0705276
sample estimates:
  mean in group Old mean in group Young 
           2.994162            3.514574

Two-sample, independent t-test

Student’s t-test with variance assumed equal

t.test(response ~ age, data = my_data1, var.equal = TRUE)

    Two Sample t-test

data:  response by age
t = -1.8791, df = 16, p-value = 0.07857
alternative hypothesis: true difference in means between group Old and group Young is not equal to 0
95 percent confidence interval:
 -1.10751153  0.06668926
sample estimates:
  mean in group Old mean in group Young 
           2.994162            3.514574

Paired t-test

t.test(my_data_paired$time_1, my_data_paired$time_2, paired = TRUE)  # works with columns

    Paired t-test

data:  my_data_paired$time_1 and my_data_paired$time_2
t = -1.7343, df = 17, p-value = 0.101
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -0.67372926  0.06580605
sample estimates:
mean difference 
     -0.3039616

Non-parametric t-tests

One-sample Wilcoxon signed rank test

wilcox.test(my_data$response, mu = 3)

    Wilcoxon signed rank test with continuity correction

data:  my_data$response
V = 1202, p-value = 7.747e-05
alternative hypothesis: true location is not equal to 3

Two-sample, independent Wilcoxon rank sum test

wilcox.test(my_data_between$Old, my_data_between$Young)  # works with columns

    Wilcoxon rank sum exact test

data:  my_data_between$Old and my_data_between$Young
W = 19, p-value = 0.06253
alternative hypothesis: true location shift is not equal to 0
wilcox.test(response ~ age, data = my_data1)  # and with formulas

    Wilcoxon rank sum exact test

data:  response by age
W = 19, p-value = 0.06253
alternative hypothesis: true location shift is not equal to 0

Paired Wilcoxon signed rank test

wilcox.test(my_data_paired$time_1, my_data_paired$time_2, paired = TRUE)  # works with columns

    Wilcoxon signed rank exact test

data:  my_data_paired$time_1 and my_data_paired$time_2
V = 49, p-value = 0.1187
alternative hypothesis: true location shift is not equal to 0

ANOVAs

Non-parametric (Kruskal-Wallis test)

kruskal.test(response ~ time, data = my_data)

    Kruskal-Wallis rank sum test

data:  response by time
Kruskal-Wallis chi-squared = 2.088, df = 2, p-value = 0.352

Factorial ANOVA

aov(response ~ gender, data = my_data)
Call:
   aov(formula = response ~ gender, data = my_data)

Terms:
                   gender Residuals
Sum of Squares   0.698464 19.651568
Deg. of Freedom         2        51

Residual standard error: 0.6207454
Estimated effects may be unbalanced
# need to use summary to see ANOVA table
summary(aov(response ~ gender, data = my_data))  
            Df Sum Sq Mean Sq F value Pr(>F)
gender       2  0.698  0.3492   0.906   0.41
Residuals   51 19.652  0.3853

Main effects

# use + for multiple main effects (only)
summary(aov(response ~ gender + age, data = my_data))  
            Df Sum Sq Mean Sq F value Pr(>F)
gender       2  0.698  0.3492   0.898  0.414
age          1  0.196  0.1959   0.503  0.481
Residuals   50 19.456  0.3891

Interaction

# use : for interaction (only)
summary(aov(response ~ gender:age, data = my_data))  
            Df Sum Sq Mean Sq F value Pr(>F)
gender:age   5  1.543  0.3087   0.788  0.564
Residuals   48 18.807  0.3918

Main effect and interaction

# string them all together
summary(aov(response ~ gender + age + gender:age, data = my_data))  
            Df Sum Sq Mean Sq F value Pr(>F)
gender       2  0.698  0.3492   0.891  0.417
age          1  0.196  0.1959   0.500  0.483
gender:age   2  0.649  0.3245   0.828  0.443
Residuals   48 18.807  0.3918               
# use * for both main effects and interaction
aov_test <- aov(response ~ gender * age, data = my_data)  
summary(aov_test)
            Df Sum Sq Mean Sq F value Pr(>F)
gender       2  0.698  0.3492   0.891  0.417
age          1  0.196  0.1959   0.500  0.483
gender:age   2  0.649  0.3245   0.828  0.443
Residuals   48 18.807  0.3918

Post-hoc comparisons

{multcomp} package for more options

TukeyHSD(aov_test)
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = response ~ gender * age, data = my_data)

$gender
                        diff        lwr       upr     p adj
Male-Female      -0.21361569 -0.7182284 0.2909970 0.5656428
Nonbinary-Female  0.04805204 -0.4565606 0.5526647 0.9712021
Nonbinary-Male    0.26166774 -0.2429449 0.7662804 0.4278041

$age
               diff       lwr       upr     p adj
Young-Old 0.1204545 -0.222078 0.4629871 0.4829496

$`gender:age`
                                      diff        lwr       upr     p adj
Male:Old-Female:Old           -0.299759805 -1.1755050 0.5759854 0.9103597
Nonbinary:Old-Female:Old       0.225248379 -0.6504968 1.1009936 0.9723190
Female:Young-Female:Old        0.181156021 -0.6945892 1.0569012 0.9894963
Male:Young-Female:Old          0.053684436 -0.8220608 0.9294297 0.9999705
Nonbinary:Young-Female:Old     0.052011732 -0.8237335 0.9277570 0.9999748
Nonbinary:Old-Male:Old         0.525008184 -0.3507370 1.4007534 0.4883543
Female:Young-Male:Old          0.480915826 -0.3948294 1.3566611 0.5834600
Male:Young-Male:Old            0.353444241 -0.5223010 1.2291895 0.8357157
Nonbinary:Young-Male:Old       0.351771537 -0.5239737 1.2275168 0.8384092
Female:Young-Nonbinary:Old    -0.044092358 -0.9198376 0.8316529 0.9999889
Male:Young-Nonbinary:Old      -0.171563943 -1.0473092 0.7041813 0.9918118
Nonbinary:Young-Nonbinary:Old -0.173236647 -1.0489819 0.7025086 0.9914384
Male:Young-Female:Young       -0.127471585 -1.0032168 0.7482736 0.9979705
Nonbinary:Young-Female:Young  -0.129144289 -1.0048895 0.7466009 0.9978402
Nonbinary:Young-Male:Young    -0.001672704 -0.8774179 0.8740725 1.0000000

Repeated measures ANOVA

# make subject within-subject factor (random effect)
summary(aov(response ~ time + Error(subject), data = my_data))  

Error: subject
          Df  Sum Sq Mean Sq F value Pr(>F)
Residuals  1 0.04394 0.04394               

Error: Within
          Df Sum Sq Mean Sq F value Pr(>F)
time       1  0.072  0.0718   0.181  0.672
Residuals 51 20.234  0.3968

Repeated measures ANOVA with interaction

summary(aov(response ~ age * time + Error(subject), data = my_data))

Error: subject
    Df  Sum Sq Mean Sq
age  1 0.04394 0.04394

Error: Within
          Df Sum Sq Mean Sq F value Pr(>F)  
age        1  0.159  0.1592   0.429  0.516  
time       1  0.072  0.0718   0.193  0.662  
age:time   1  1.878  1.8782   5.057  0.029 *
Residuals 49 18.197  0.3714                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

{afex} package

Try {afex} for powerful ANOVA and linear modeling functions

library(afex)
aov_ez(id = "subject", dv = "response", between = "age", 
       within = "time", data = my_data)  
Anova Table (Type 3 tests)

Response: response
    Effect          df  MSE      F  ges p.value
1      age       1, 16 0.33   0.60 .011    .451
2     time 1.88, 30.02 0.40   1.17 .048    .323
3 age:time 1.88, 30.02 0.40 2.61 + .102    .093
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Sphericity correction method: GG 
# by default, this uses type III sums of squares, like SPSS

Type II sums of squares

aov_ez(id = "subject", dv = "response", between = "age", 
       within = "time", data = my_data, type = 2)  
Anova Table (Type 2 tests)

Response: response
    Effect          df  MSE      F  ges p.value
1      age       1, 16 0.33   0.60 .011    .451
2     time 1.88, 30.02 0.40   1.17 .048    .323
3 age:time 1.88, 30.02 0.40 2.61 + .102    .093
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Sphericity correction method: GG 
# but can set sums of squares, like II, which is what R uses by default

Let’s code!

Statistics 1